Not Available: Give Some Thought to Missing Data

During my undergrad, missing data was not a subject that was ever discussed. For the uninitiated, the choice to restrict an analysis to complete observations (those with no missing values) may be an unconscious decision. However, it does not take too much thought to understand how this could lead to misleading conclusions.

Types of Missing Data

Imagine we are studying quality of life in over 50s. We randomly select 1000 over 50s from some imaginary data source that has the age of an individual and their address, and we send them a quality of life survey. We only receive 850 completed surveys back. We do some digging, and the average age of individuals who did not respond is greater than those that did respond. This is a problem because our sample is no longer a random sample of all over 50s. It is biased towards younger individuals.

This has implications for what we learn from the data. For example, age may be negatively correlated with quality of life: individuals who are older tend to report a lower quality of life. Thus, our biased sample may lead us to conclude that over 50s have a higher quality of life than they actually do. When missing data are correlated with observed values they are known as missing at random (MAR) (Donders et al., 2006).

Most missing data are MAR, but there are two other categories of missing data. For example, if 100% of individuals returned their surveys but we lost 150 of them during an office move, this would introduce missing data but not necessarily bias our analysis. The surveys that were lost were totally random, and thus the remaining sample is still a random sample of the larger population. These data are known as missing completely at random (MCAR).

Now imagine the age is not correlated with quality of life. Only 850 of our 1000 invited participants return their survey. Unknown to us, the 150 individuals that didn’t return their survey have a very poor quality of life because they suffer from chronic illness. This will bias our analysis as before, but we are completely blind to this fact because we don’t have any data on participant’s health, or even any variable that is correlated with chronic illness. Such data are called missing not at random (MNAR).

Single Imputation

Clearly, just keeping complete observations in an analysis leaves us exposed to potential bias if data are MNAR or MAR. In the former case, there is little that we can do to remedy the situation, but in the latter, there is the possibility of imputing missing values. In simple terms, this involves predicting what a missing value should be, based on the other data that we have available to us.

This imputation can be fast and simple. For example, filling in missing values with the mean of that variable or other similar observations’ value for that variable. However, these crude methods of imputation may erode relationships between variables; artificially reduce standard errors and confidence intervals; and/or fail to alleviate bias.

More complex imputation methods for missing data involve statistical models. The simplest of these is regression: the missing data for a variable are predicted by a regression equation describing the relationship of other variables in the data to that variable. In our example of the quality of life survey, we have just one predictor (age) so we can visualise the regression with a ‘best fit’ line:

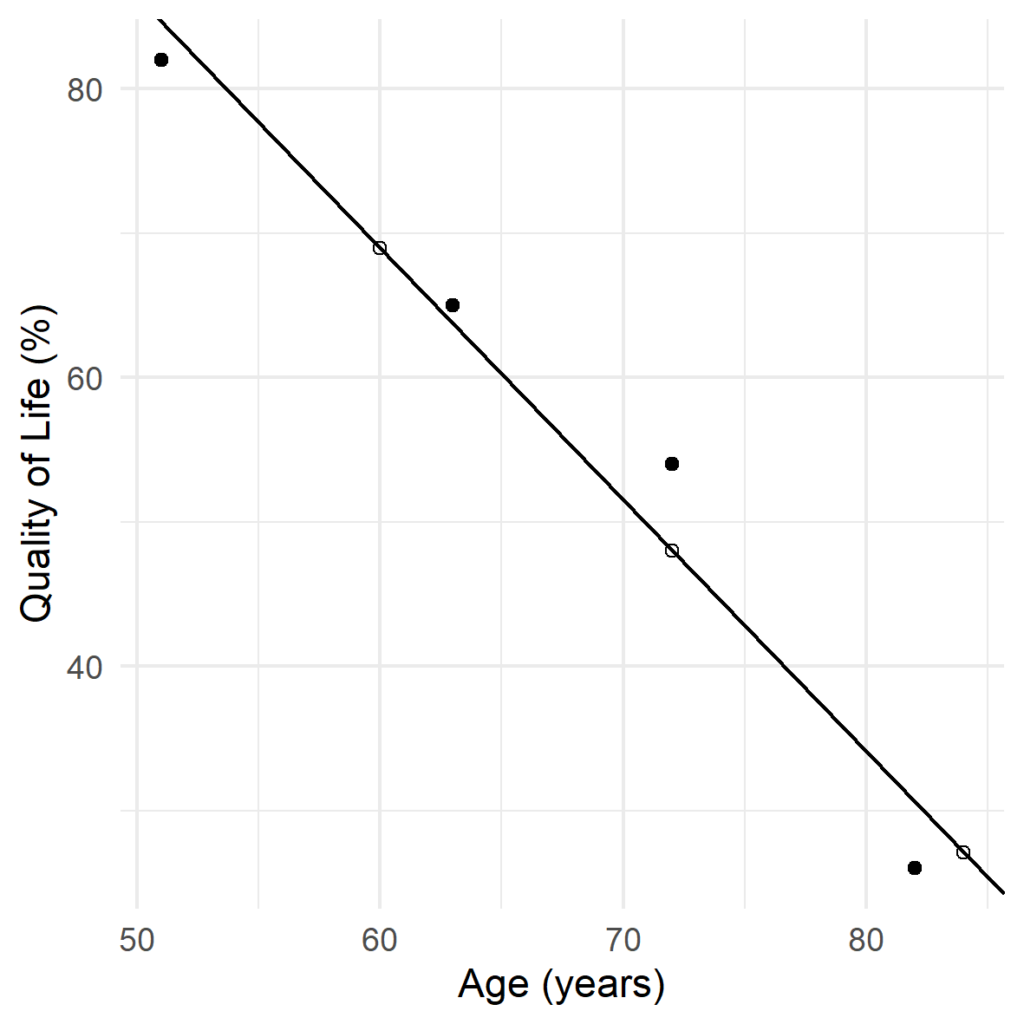
This graphical representation also allows us to visualise why using regression for imputation introduces bias. By assuming that the imputed point falls on the regression line, we expect a correlation of 1 between age and quality of life! In reality, this is not the case: if we observed the data point, it is most likely that it would be somewhere close to the regression line, but not on it exactly. This is because quality of life is affected by factors other than age, like health, which aren’t fitted in the regression model. Thus, by using regression we artificially reduce the variance of the quality of life score, increase the correlation with age, and bias any analyses we perform (Donders et al., 2006; Uh et al., 2008).

Regression imputation is an example of a single imputation method because it produces just a single imputed value for every missing value. An alternative type of single imputation exploits the random forest algorithm. As single imputation methods, regression and random forest imputation are limited because they do not take into account the uncertainty in the imputed values. We then carry the imputed values into any analysis as if they were true, observed values: leading us to be more certain about the outcome our analysis than we probably should be.

However, unlike regression, random forest imputation is unbiased, and confers numerous advantages such as being non-parametric and able to work on data of different types simultaneously. In brief, random forest imputation inserts placeholder values where there are missing data and, one variable at a time, reverts these to missing values and imputes them based on all of the other data using the random forest algorithm. This is repeated many times until the imputed values reach some stopping criteria, with the accuracy of imputation improving with each iteration. Random forest imputation can be performed using the missForest R package (Stekhoven & Bühlmann, 2012). Below I give the code I use to run missForest in parallel as it is resource demanding and the vignette does not have an example.

library(doParallel)
library(missForest)

# replace *** with the number of variables in your data or the number of cores available to you,
# whichever in smaller
c1 <- makeCluster(***, outfile = "")
# outfile = "" helps you keep an eye on your workers
registerDoParallel(c1)

imputed_data <- missForest(your_data, parallelize = "variables")

Multiple Imputation

To overcome the limitations of single imputation methods, we can use multiple imputation. As its name suggests, multiple imputation performs imputation multiple times, allowing assessment of the uncertainty that is associated with imputation.

Multiple imputation by chained equations (MICE) is a popular multiple imputation technique. Somewhat similarly to random forest imputation, it first inserts placeholder values where there is missing data, and then works through each variable in turn. MICE produces a regression model for each variable, replaces the placeholders for the variable with missing data, and predicts them based on the regression. Once the imputed values converge, we have a complete, imputed data set. The multiple aspect comes in when we then repeat this process between 5 and 40 times to produce additional, complete, imputed data sets.

You can now run whatever analysis is was you intended to run - but instead of running it once, you run it on every imputed data set you have created. Then, the outputs of each analysis are combined to give the final result. This “combining” can be done for you by software for most standard statistical tests, but may be something you need to work out for yourself if you are using a non-standard analysis method (Azur et al., 2011).

missForest and MICE should cover most of your imputation needs. Of course, in practice, you’ll no doubt still find yourself scratching your head sometimes. How much missing data is too much missing data for imputation? How many data sets should I impute using MICE? How do I even know that my data are MAR to begin with? (Because if they are not, imputation may not be helpful at all!)

It’s natural to have questions, because how we should treat missing data is still an active area of research: an area of research that’s dealing with a tough statistical and philosophical dilemma - how do we deal with what we do not know?

References

Azur, M. J. et al. (2011) ‘Multiple imputation by chained equations: What is it and how does it work?’, International Journal of Methods in Psychiatric Research. John Wiley & Sons, Ltd, 20(1), pp. 40–49. doi: 10.1002/mpr.329.

Donders, A. R. T. et al. (2006) ‘Review: A gentle introduction to imputation of missing values’, Journal of Clinical Epidemiology. Pergamon, 59(10), pp. 1087–1091. doi: 10.1016/j.jclinepi.2006.01.014.

Stekhoven, D. J. and Bühlmann, P. (2012) ‘Missforest-Non-parametric missing value imputation for mixed-type data’, Bioinformatics. Oxford Academic, 28(1), pp. 112–118. doi: 10.1093/bioinformatics/btr597.

Uh, H. W. et al. (2008) ‘Evaluation of regression methods when immunological measurements are constrained by detection limits’, BMC Immunology. BioMed Central, 9, p. 59. doi: 10.1186/1471-2172-9-59.