Unpacking GREML (#1): Heritability and Mixed Linear Models
Heritability is a central concept in quantitative genetics. Yet estimating the heritability of a trait is not straightfoward. There are a wide range of different approaches to heritability estimation. This series takes a look at how one of these methods, GREML, functions under the hood.
I started my PhD knowing literally nothing about heritability estimation. I have found the journey to understand this topic to be surprisingly challenging. This was partly because I encountered a lot of concepts that I hadn’t come across before, but was also confounded by implicit assumptions, unsettled debates, and confusing nomenclature.
This is the first of three blog posts where I’ll summarise my understanding of one of many methods of heritability estimation: genomic restricted maximum likelihood (GREML). I intend these posts to be an informal tutorial, peppered with heuristic examples that have aided my understanding, aimed at those with a background in biology but no knowledge of heritability estimation. In this post I give an overview of heritability and give a gentle introduction to the basic statistical concepts you’ll need to understand it. In part two, I’ll dive deeper into how GREML addresses specific challenges associated with heritability estimation, and the final part will describe variations on the GREML method.
So what is heritability? Heritability could be described as a measure that allows us to assess the relative contribution of genetic and non-genetic factors to a trait. More formally, heritability is defined as the proportion of the trait variance () that is explained by additive genetic variance () (Eqn 1). By additive, I am referring to loci where the phenotype of the heterozygote is the intermediate of the homozygotes. Dominance is a whole other topic that I will not touch on here.
Importantly, heritability is not a feature of a trait. Rather, it is a feature of a population at a specific time point. Heritability differs over different populations and times as a consequence of any change in the environment (may affect the phenotypic variance) or the genetic composition of the population (may affect the genetic variance).
Heritability is of particular interest in animal breeding as it can be used to predict the response to artificial selection. A crude approach to artificial selection would be, say, to cross the trees with the greatest height with each other to produce taller trees. This approach assumes that taller trees carry genetic variants that predispose greater height. What about a case where a tree is taller because of some environmental factor? This isn’t transmissible to the offspring of this tree. Another feature of GREML, other than providing us with heritability estimates, is assigning individuals breeding values: a measure of their genetic merit that can be used to pick out the best breeding prospects.
The reason for this is that GREML’s roots are in animal breeding. It is descended from other restricted maximum likelihood (REML) approaches that used pedigree data (instead of genetic data) in animal populations to estimate genetic variance and predict breeding values.
Interest in heritability extends out of animal breeding into the field of medical genetics. Let’s revisit the earlier statement that heritability is ‘a measure that allows us to assess the relative contribution of genetic and non-genetic factors to a trait’. Such a measure would be useful when trying to understand what factors cause disease. In the last decade many genes have been associated with human traits, giving us insight into their underlying biology.
Such studies have provided us with large cohorts of participants genotyped at a huge number of single nucleotide polymorphisms (SNPs). These data sets can be used to estimate heritability of traits in human populations using GREML.
So what is GREML? Here is already a potential source of confusion over nomenclature. REML is just a statistical approach used to obtain a variance estimate from a linear regression model. GREML refers to a mixed linear regression model with phenotype as the response variable and genotypes as regressors, where REML is used to estimate the genetic variance component. In a lot of places, you will see the term GREML used to refer to a specific type of GREML implemented in the software package GCTA (more on this in part three). I’ll personally avoid this because GCTA-GREML is not the only heritability estimation method that uses REML with genomic data, thus I find the term GREML to refer to just one subtype of genomic REML potentially misleading.
Let’s start by unpacking what a mixed linear regression is. A graph like this probably pops into your head (Fig 1):
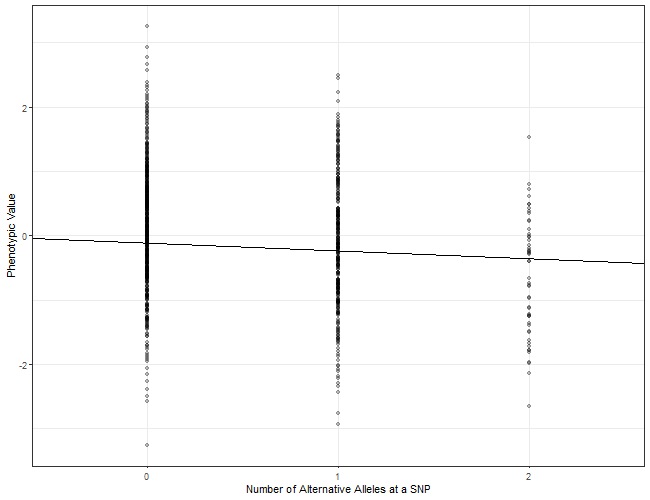
Figure 1 | Example of a regression line regressing allele dosage at a SNP on phenotype.
As it’s relevant to GREML, I’m going to run with the example of regressing SNPs on a phenotype. It’s important to get comfortable with the mathematical expression of a linear regression (Eqn 2):
In such a linear regression, we use the number of alternative alleles carried at a SNP as a predictor () of the phenotypic value (). is the y-intercept of the regression line, and is the slope of the regression line (which is an estimate of the effect of the SNP on the phenotype). The residual () is the variation in the phenotype that cannot be explained by this SNP.
In genetics, we have many SNPs to use as predictors, so we expand this to matrix vector form (Eqn 3, 4 are equivalent):
We have phenotypic records in our model (for simplicity, we’ll assume that every individual has a single phenotypic record, thus the number of individuals is equal to the number of phenotypic records). We have SNPs to use as predictors, meaning that we will need to estimate regression coefficients () for each one of these SNPs. is a design matrix that relates every phenotypic record to the number of alternative SNP alleles carried by the individual that phenotypic record belongs to at each SNP. Thus, it is a matrix of individuals by SNPs in this case ( x ). Finally, the column vector represents the residual: the part of each record that we can’t explain using the SNP predictors.
From this, we can say that our phenotype is distributed where is an ( x ) identity matrix. To give you a rough intuition for what this means: phenotypic values are normally distributed (this is an assumption of a linear regression); the phenotypic mean for individuals with particular genotypes is dependent on the effects of those SNPs on the phenotype; but even individuals of identical genotypes vary around the mean because of factors that we have not accounted for, which are contained within the residual, and thus described by the variance of the residual ().
You might ask: where the did come from?! This leads us nicely into a discussion about fixed and random effects. In the regression I described above, is more accurately described as a vector of fixed SNP effects. The distinction between fixed and random effects can be troublesome to describe. I shall give a rough definition that is suitable for grasping GREML, but when faced with a decision of designating an effect as fixed or random, you should not use this as a rule: consult other sources instead (such as Gelman & Hill, 2007, pg 245).
We can think of random effects as effects that are drawn from an underlying distribution. There will be some sampling variance associated with drawing the effect from the distribution (this is what describes). The shape of this distribution is up to you to decide: whilst discussing GREML we will always assume that random effects are drawn from multivariate normal (MVN) distributions.
In contrast, fixed effects are not randomly selected from a distribution. Sex is often treated as a fixed effect: individuals are either male or female, their phenotype is affected by being either male or female, and there is no sampling variance associated with this.
When discussing GREML, we tend to think of SNP effects as random rather than fixed. This has several benefits. First, we are interested in variance of the genetic effects: this gives us an estimate of the genetic variance which we can then use to calculate the heritability!
Second, genomic datasets tend to have far many SNP predictors than they do phenotypic records. Having more predictors than observations ( > ) poses statistical challenges. It may cause your model to be overfit to your data. In other words, the model is good at predicting the effects of SNPs in the sample of individuals you fitted it on, but these effects are not generalisable to the wider population. Additionally, it means there is no unique solution to the mixed linear model equation (i.e. it is difficult to solve for ). In the next installment of this series I’ll discuss from a more mathematical perspective why such problems arise and how we combat them.
For completeness, this is what a typical GREML equation looks like when we have n phenotypic observations, SNPs, and m other predictors (such as sex, age etc.) which we will treat as fixed:
Where:
- is the ( x 1) vector of phenotypic observations;
- is the ( x ) design matrix for fixed effects;
- is the ( x ) design matrix for random SNP effects;
- is the ( x 1) vector of vector of random SNP effects distributed MVN(0,)s;
- is the ( x 1) vector of fixed effects;
- is the ( x 1) vector of random residual effects distributed MVN(0, ).
In part two, I’ll discuss how this equation is actually used to obtain estimates of SNP effects and the genetic variance.
References
Mrode, R. A. (2005) Linear Models for the Prediction of Animal Breeding Values, 2nd ed., Oxford: CABI Publishing.
Gelman, A. & Hill, J. (2007) Data Analysis Using Regression and Multi-level/Hierarchical Models, 1st ed., Cambridge, UK: Cambridge University Press.